8.- ¿Por qué no cae la Luna como la manzana si están atraídas por el mismo tipo de fuerza?

Tenemos que diferenciar que no toda clase de masa o sustancia genera gravedad. La manzana no tiene poder de atracción sobre nada y mucho menos sobre la Tierra. La manzana cae al suelo sólo por la fuerza de atracción que desarrolla la gravedad de la Tierra, no por ninguna fuerza que pueda desarrollar la manzana, exactamente le sucede igual a las rocas, al agua, la a arena, a la madera, etc, son masas muertas que no generan gravedad, sólo sufren la atracción que desarrollan los cuerpos que sí desarrollan gravedad.
Así que la idea que Newton tenía sobre la gravedad, no era correcta; en este sentido Newton estaba equivocado, pues la manzana no atrae a la Tierra en la misma forma que la Tierra atrae a la manzana.

En definitiva, la manzana caerá como resultado de la atracción que ejerce la tierra sobre ella, en cambio, la luna no caerá porque ejerce su propia fuerza.

Para explicarlo ponemos este ejemplo: La rotación de la Luna alrededor de la Tierra se parece al giro de una pelota atada al extremo de una cuerda; trata de moverse en línea recta (como lo haría si la cuerda se rompiera), pero la cuerda la mantiene girando en círculos. Imaginemos que la gravedad de la Tierra es el trozo de cuerda. La velocidad de la Luna, basta para impulsarla al espacio, pero la gravedad de la Tierra, que disminuye con la distancia, tiene la potencia suficiente para mantenerla en órbita.

7.- Explica de qué tratan cada uno de los libros de Principia.

Los principia forman un conjunto de tres libros que son la eminencia de las obras de la época. Su nombre original era: "Philosophiæ naturalis principia mathematica" (Principios matemáticos de filosofia natural).En los tres volúmenes de los Principia Newton presenta no sólo la ley de gravitación universal sino las famosas "Leyes de Newton" sobre le movimiento de los cuerpos y las fuerzas que los determinan.

Los libros tratan de distintos temas:

• Primer Libro: Retoma los temas ya presentes en De Motu (anterior libro de Newton). En él se describe, en efecto la teoría general de la dinámica, y dentro de ella las leyes fundamentales sobre el movimiento y la fuerza de la energía. Las demostraciones que incluye tienen formulación esencialmente teórica, por que examina el movimiento de los cuerpos sin masa, puntiformes, que se mueven en un medio que no opone ninguna resistencia al movimiento, en una situación por lo tanto inexistente en la naturaleza.
  

• Segundo Libro: es el menos destacado y trata del movimiento de partículas en un medio resistente y en él se demuestra que las leyes generales expuestas en el libro primero son validas también en el mundo de las experiencias terrestres, en donde todo movimiento se produce en un medio fluido, así se trate de aire o de agua.

• Tercer Libro: es la parte mas relevante de toda la obra, ya que en él Newton expone los principios de los movimientos celestes mediante las teorías generales de la dinámica y con ello enlaza sistemáticamente la dinámica con la astronomía. Es la primera vez que esto ocurre en la ciencia.

6.- Explica en qué consiste el cálculo diferencial establecido por Newton y Leibniz. ¿Qué importancia tiene esa manera de estudiar los fenómenos?

Función del cálculo diferencial

El cálculo diferencial, tuvo su origen en dos grandes científicos: Leibniz y Newton. Al principio no se supo con certeza cual de los dos había sido el descubridor original. Más tarde se supo que ambos lo eran, porque habían llegado a los mismos resultados de forma diferente. Pero la función del cálculo diferencial propiamente dicho es que, gracias a esto podemos averiguar que es lo que está sucediendo en una situación, en cada instante

Las conclusiones fueron:

El cálculo diferencial, se consolidó como disciplina matemática principalmente en los siglos XVI y XVII cuando Leibniz, Galileo y Newton entre otros, intentaron estudiar los distintos tipos de movimiento, en general los de cambio y describir la velocidad instantánea de un cuerpo en movimiento.

Con el descubrimiento del cálculo diferencial se creó el concepto de derivada, que fue desarrollado por Leibniz y Newton. Leibniz fue el primero en publicar la teoría, pero parece ser que Newton tenía papeles escritos (sin publicar) anteriores a Leibniz. Debido a la rivalidad entre Alemania e Inglaterra, esto produjo grandes disputas entre los científicos proclives a uno y otro pais. Leibniz llegó al concepto de derivada estudiando la velocidad de un móvil y Newton llegó a este mismo concepto al que llamaba fluxiones estudiando las tangentes.

A partir de Leibniz y Newton el cálculo diferencial siguió desarrollándose y avanzando hasta la actualidad, siendo notable incluso en el día a día.

La importacia que tiene, es que ha tenido efectos muy importantes en casi todas las áreas de la vida moderna: es fundamento para el cálculo numérico aplicado en casi todos los campos técnicos y/o científicos cuya principal característica es la continuidad de sus elementos, en especial en la física. Prácticamente todos los desarrollos técnicos modernos como la construcción, aviación, transporte, meteorología, etc. hacen uso del cálculo. Muchas fórmulas algebraicas se usan hoy en día en balística, calefacción, refrigeración, etc.

Leibniz (1646/1716)-------------------- Newton (1643/1727)

5.EXPLICA LA FORMACIÓN DEL ARCO IRIS EN BASE A LA FIGURA 4.9 DEL LIBRO

Al igual que en un prisma el agua tiene la capacidad de descomponer la luz blanca en diferentes colores. Una parte de la luz atraviesa la gota y se pierde, mientras que la otra rebota en el interior de la gota y nuevamente en un cierto ángulo. Finalmente, la luz sale disparada en diversos colores en cualquier dirección. Estos son los que podemos ver.

La luz se puede reflejar en una gota, pero para contemplar la formación de un arco iris, es necesario que en un conjunto de gotas, los rayos solares incidan sobre ellas formando el mismo ángulo y con esto se disponen en un arco perfecto, dando lugar al arco iris primario.

También existe otro tipo de arco iris, el arco secundario, formado por gotas que se encuentran en diferentes posiciones al primario, por lo que la luz incidirá en ellas desde un ángulo diferente.

Se pueden diferenciar a simple vista ya que el arco secundario es más exíguo que el primario.

4.- ¿A qué conclusiones llegó Newton con su famoso experimento del prisma?

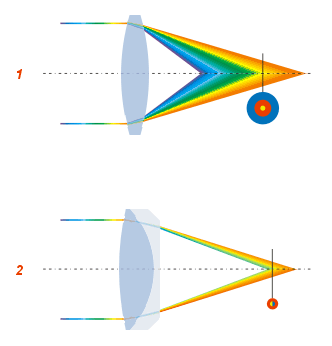
El experimento del prisma está dividido en varias fases, a continuación las explicaremos brevemente para saber a que conclusiones llego en cada una de ellas y cual es su conclusión final.

• La primera fase consistió en: oscureció su habitación dejando pasar un pequeño haz de luz por un agujero donde colocó el prisma. La luz, al pasar por el prisma se proyectó de forma oblonga, lo que sorprendió a Newton ya que de acuerdo con las leyes de refracción se esperaba una forma circular. Con lo cual llegó a dos posibles conclusiones: que el prisma es el que aporta los colores a la luz, o bien, que la luz está compuesta por todos los colores del arcoiris y el prisma los separa.
  


• Segunda fase: Cogió dos trozos de hilo, uno rojo y otro azul, les hizo un nudo y al observarlos a través del primas vió que el hilo rojo parecía estar adelantado al azul. Con esto concluyó diciendo que: en el interior del prisma cada color tiene una velocidad propia (longitud de onda). Además pudo descartar una de las conclusiones de la primera fase, porque quedó claro que los colores no son una propiedad del objeto.
  


• Tercera fase: Presenta los dos experimentos anteriores en la Royal Society, pero avanza un paso más. Girando él mismo un prisma va eligiendo los colores a mostrar, uno de ellos predomina, pero no esta completamente limpio. Al reflejarse en otro prisma, podemos ver únicamentes ese color y de forma circular. Con esto reafirma las conclusiones anteriores que decían que los colores estaban concentrados en la luz blanca y el primas lo único que hacia era dividirlos.
  

• Cuarta fase: La prueba definita que permite concluir con éste experimento consiste en que una vez realizada la descoposición de los colores, se reflejan en una pantalla donde éstos se funden, y al reflejarse en otra pantalla cercana, la luz es blanca de nuevo. Por tanto, la conclusión final es: La luz es una mezcla de todos los colores que los prismas son capaces de separar, del mismo modo que los prismas los separan, al chocar con las paredes se funden produciendo otra vez la luz blanca inicial.

3.- ¿Qué diferencias existen entre el telescopio diseñado por Newton y el de Galileo? Busca qué es eso de la aberración cromática.

Telescopio de Galileo.

1. En el montaje del telescopio Galileo y Newton utilizarón diferentes materiales: el primero utilizó lentes, y el otro espejos.
2. El telescopio de Galileo tenia una calidad de imagen menor, debido a un efecto denominado aberración cromática*, mientras que el de Newton no tenia este problema gracias al uso de los espejos.
3. El telescopio de Galileo tenía una lente objetivo convexa y una ocular cóncava, con lo que producía imágenes no invertidas y virtuales, en cambio, Newton colocó un espejo esférico en la parte baja del tubo y recogió los rayos reflejados en un espejo secundario, que reflejaba la luz a una lente convexa colocada en un tubo exterior que hacía de ocular.
   
6. Telescopio de Newton.

4. El telescopio de Galileo tiene un objetivo plano-convexo (la lente hacia el objeto) con una distancia focal entre 75 y 100 cm., y un visor plano-cóncavo con una distancia focal de unos cinco centímetros, sin embargo, los reflectores como el de Newton se constituyen de un espejo principal (espejo primario u objetivo), el cual no es plano como los espejos convencionales, sino que fue provisto de cierta curvatura (idealmente parabólica) que le permite concentrar la luz en un punto y tiene una distancia focal mayor.

5. El telescopio de Galileo posee un visor que está en un pequeño tubo que puede ajustarse para el enfoque. La ampliación del instrumento era de unos 15 a 20 aumentos. Newton consiguió doblar la cantidad de aumentos y además en un telescopio de menor longitud que el de Galileo, ya que el de éste era de metro y medio y el de Newton de apenas quince centímetros.

6. El telescopio de Newton puede ser algo más frágil y caro de mantener porque habría que cambiar los espejos cada cierto tiempo, mientras que en el de Galileo las lentes aguantarían más.

* Aberración cromática: Un segundo desarrollo teórico llegó en 1672, cuando Isaac Newton publicó su celebrado papel la luz y el color. Newton demostró que la luz blanca es una mezcla de luces coloreadas de distinto grado de refracción (distintos colores). El resultado fue que cualquier lente curva podía descomponer la luz blanca en los colores del espectro, cada una yendo a focos distintos en el eje axial. Este efecto se conoce como aberración cromática.

2.- ¿Qué significa la frase "Amicus Plato amicus Aristoteles magis amica veritas" y qué quería decir con ella Newton?

Literalmente significa:

Platón es mi amigo, Aristóteles es mi amigo, pero mi mejor amiga es la verdad>

Tras haber leido el libro, creemos entender mejor a Newton, por lo para nosotras la frase significa:

La ciencia siempre está en movimiento, es decir, lo que es verdad hoy puede no serlo mañana. Conocer el pasado ayuda a no cometer los mismos errores en el presente, por esto menciona a Platon y Aristóteles, ya que para Newton ellos fueron la base, y como se menciona en el libro, los hombros en los que se apoyó para acercarse lo máximo posible a la verdad.

• En definitiva, la frase quire decir que Newton se apoya en teorías pasadas, a partir de las cuales, mejorándolas y aplicando su propio conocimiento intenta responder a una pregunta común, e intenta que la respuesta dada sea una verdad inmutable. Por este úlitmo hecho, la frase nos dice que la verdad es su mejor amiga.

1.- ¿Quién fue y en qué ayudó a Newton un tal Clark?

Casa de Newton en Woolsthorpe

Después de la muerte de su padrastro (reverendo Smith), la familia volvió a reunirse, y Newton se encontró viviendo con sus hermanastros, su abuela y su madre. Este hecho no fue aceptado por Newton, quien fue a estudiar a la escuela de gramática de Grantham. A pesar de la cercanía de su pueblo, se hospedó en la casa del boticario del pueblo, Clark.

Si bien Newton no prestó demasiada atención a Clark (hecho facilmente observable ya que Newton solo lo menciona una vez), sí que la prestó a los procedimentos y utensilios con los que Clark ejercía su profesión (fabricar mejunjes y medicinas). Pero Clark volvió a ser relevante posteriormente en la vida de Newton, recomendándolo a un profesor, que era amigo suyo y que trabajaba en el Trinity College, lo que permitió a Newton obtener una de las nueve becas que se concedían.

9. Opinión Personal

No sabíamos si ponértelo o no pero al final creemos que está bien que sepas como hemos entendido el capítulo.

Este capítulo nos ha parecido, por lo general, bastante entretenido, ya que, aunque era muy largo, (y había algunas partes que se hacían eternas) estaba escrito de una manera muy amena, con un vocabulario bastante fácil de entender. El autor trata de transmitirnos lo que pensaban los personajes, intenta que nos sintamos un poco identificados, con frases como “A ver qué hace don Vicenzo con semejante zascandil. Por lo menos echarle una bronca en condiciones…”, y son este tipo de detalles los que, en mi opinión, hacen la lectura mucho más amena y divertida. Además, el autor nos ha dado muchísimos datos sobre la biografía de Galileo. Nos ha contado muchos detalles de su vida, de su forma de ser, de sus experimentos, invenciones y descubrimientos… Nunca nos hubiéramos imaginado que la vida de Galileo fue así, ni que tenía esa personalidad, irónica y desenvuelta… Este tipo de cosas me han resultado muy curiosas, y le han dado un toque de gracia al capítulo.

8. Haz un guión de prácticas (objetivo, material necesario, montaje, medidas a tomar) de cómo reproduciríais el experimento de los planos inclinados.

Objetivo:

Comprobar por nosotros mismos que lo que dijo Galileo era cierto, es decir, demostrar que el tiempo que un objeto tarda en caer por un plano inclinado no es proporcional a la distancia que recorre.

Material necesario:

• Panel de conglomerado (6m aprox)


• Liston de madera


• Taladro


• Tornillos


• Tacos


• Canicas


• Escalímetro


• Cronómetro


• Papel milimetrado


• Lápiz


• Lámina de metal (de pequeño tamaño)

Montaje:

Lo primero es conseguir un aglomerado y con el taladro hacemos un agujero en cada uno de los lados de uno de sus extremos, así como en cada uno de los listones de madera.

Insertamos los tacos y tras ello los tornillos, aplicando un poco de presión para comprobar que el montaje resista.

Utilizando el escalimetro, marcamos en el tablón de conglomerado las cuatro medidas propuestas en el libro (6oocm, 450cm, 300cm y 150cm).
A continuación uno de los miembros del grupo será el encargado de lanzar la canica por el plano inclinado ( cada vez desde una de las medida citadas anteriormente), para ello se utilizará una lamina de metal como tope para ser más precisos. Mientras, el otro será el encargado de cronometrar el tiempo que tarda la bola en descender el conglomerado y anotarlo para poder hacer gráficas más tarde.

Medidas a tomar:

• Lo primero es lijar el conglomerado para quitar posibles imperfecciones y con una brocha se le aplicará aceite para disminuir el rozamiento.


• También será necesario repetir unas treinta y cinco veces el lanzamiento de la canica desde cada una de las medidas para aumentar la precisión.

7. ¿Cómo dividió los movimientos Galileo y cuáles eran las características de cada uno de ellos?

Hacia el 1604, Galileo Galilei hizo sus famosos estudios sobre distintos movimientos, a fin de comprender aspectos del movimiento relevantes en su tiempo.

Tras mucho tiempo tomando datos, Galileo se dio cuenta de que había tres tipos de movimientos: el movimiento periódico, el movimiento rectilíneo uniforme, y el movimiento rectilíneo uniformemente acelerado.

Concluyó que la masa es independiente de la velocidad, que es cierto. Su único pequeño error fue que dijo también que dos objetos de distinta masa y tamaño caerían a la vez, ya que no tuvo en cuenta el rozamiento del aire.

Movimiento periódico

Un movimiento periódico es el tipo de evolución temporal que presenta un sistema cuyo estado se repite exactamente a intervalos regulares de tiempo.
El tiempo mínimo T necesario para que el estado del sistema se repita se llama período. Si el estado del sistema se representa por S, se cumplirá:

S(t) = S(t + T), \qquad\forall t

Dentro del movimiento periódico distinguimos varios tipos, el más significativo es el movimiento armónico simple.






Movimiento rectilíneo uniforme

Un movimiento es rectilíneo cuando el móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Fue el moviento que estudio Aristóteles en el que más se centro, y nos referimos a él mediante el acrónimo MRU.

El MRU se caracteriza por:

• Movimiento que se realiza sobre una línea recta.
• Velocidad constante; implica magnitud y dirección constantes.
• La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
• Aceleración nula.
• Solo se da en condiciones ideales en el vacio.

La ecuación del movimiento rectilíneo uniforme es:

x = x_0 + vt

Representación gráfica del movimiento




Al representar gráficamente la velocidad en función del tiempo se obtiene una recta paralela al eje de abcisas.

La representación gráfica de la distancia recorrida en función del tiempo da lugar a una recta cuya pendiente se corresponde con la velocidad.

Movimiento rectilíneo uniformemente acelerado

Evolución respecto del tiempo de la posición, de la velocidad y de la aceleración de un cuerpo sometido a un movimiento rectilíneo uniformemente acelerado, según la mecánica clásica.
El movimiento rectilíneo uniformemente acelerado (MRUA), es aquél en el que un móvil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.
Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.

En mecánica clásica el movimiento uniformemente acelerado (MRUA) presenta tres características fundamentales:

-La aceleración y la fuerza resultante sobre la partícula son constantes.

-La velocidad varía linealmente respecto del tiempo.

-La posición varía según una relación cuadrática respecto del tiempo.

Las ecuaciones del movimiento rectilíneo uniformemente acelerado es:

v = v_0 + at --------------- r = r_0 + v_0t + 1/2 at (al cuadrado)

Su representación gráfica es:

Evolución respecto del tiempo de la posición, de la velocidad y de la aceleración de un cuerpo sometido a un movimiento rectilíneo uniformemente acelerado, según la mecánica clásica.

Ahora ponemos un video para que quede más claro:

6. ¿Cómo explica la caída libre Aristóteles y cómo lo hizo Galileo?

Galileo decidió citar a un gran número de físicos y científicos de la época para que observasen su experimento y que viesen que se comprobaba su teoría negando las enunciadas anteriormente por Aristóteles. Los citó debajo de la torre inclinada de Pisa, donde él subió hasta el último piso para obtener altura suficiente. Desde esa posición dejó caer varias bolas de diferentes materiales (madera y plomo) y por lo tanto también diferentes masa y peso.

La teoría anterior de Aristóteles señalaba que llegarían al suelo con un espacio de tiempo importante entre una y otra proporcionalmente a su masa, pero Galileo demostró que no, aunque no llegaron exactamente a la vez, el espacio de tiempo que las separaba era insignificante, demostrando de esta manera que la teoría anterior no era correcta.

Antes de demostrar su teoría, Galileo realizó varias veces este mismo experimento, midiendo la distancia entre el lugar de lanzamiento y el suelo, y el tiempo que tardaban en recorrerlo. Para medir el tiempo utilizó diversas formas de medición, desde un péndulo hasta un laúd.Gracias a esto y después de hacer los cálculos pertinentes, el propio Galileo consiguió dar con el valor exacto de la gravedad, que se nombra con una G en honor a este gran científico.

Video para que quede más claro:

5. ¿De qué trata el libro "Diálogos sobre los dos grandes sistemas del mundo"?

Fue uno de los libros más importantes escritos, debido a que por su contenido, Galileo fue acusado de herejía y juzgado por la inquisición. Galileo utiliza tres personajes que a continuación explicaremos brevemente:

• Salviati: defensor del sistema copernicano. Representa la propia visión de Galileo.


• Simplicio: quien aboga por el sistema de Ptolomeo y Aristóteles. Su posición ha sido caracterizada como una sátira del mismo Papa.


• Sagredo: es un neófito inteligente que representa la visión neutral de quien busca la verdad sin aferrarse a dogma alguno, lo hace en honor a su amigo Sagredo, juzgado y ejecutado por la Inquisición.

El libro se resume en una interacción entre el sistema Ptolemaico-aristotélico y el copernicano, ya que si no hablara del primero no hubiera sido posible su publicación. Aún así, Galileo muestra una preferencia por el sistema copernicano, dando una mayor inteligencia a Salviati para defenderlo.

En definitiva, es una reflexión sobre ambos sistemas.

4. ¿Qué demostró Johannes Kepler?

Johannes Kepler fue un prestigioso científico de la época que sentía una gran admiración por Galileo, por este hecho varió sus observaciones hacia el campo matemático. Tambien fue el descubridor de que las orbitas eran elípticas por lo que enunció los siguientes postulados:

• PRIMERA LEY

Los planetas describen órbitas elípticas estando el Sol en uno de sus focos:

r1 es la distancia más cercana al foco (cuando q=0) y r2 es la distancia más alejada del foco (cuando q=p).
Una elipse es una figura geométrica que tiene las siguientes características:
Semieje mayor a=(r2+r1)/2
Semieje menor b
Semidistancia focal c=(r2-r1)/2
La relación entre los semiejes es a2=b2+c2
La excentricidad se define como el cociente e=c/a=(r2-r1)/(r2+r1)

• SEGUNDA LEY

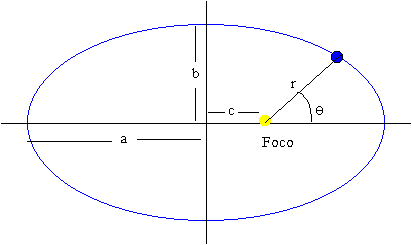
El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.

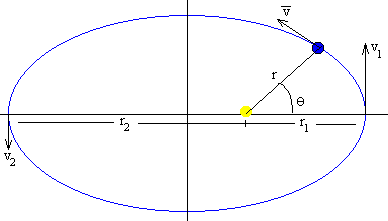
L=mr1·v1=mr2·v2

• TERCERA LEY

Los cuadrados de los periodos P de revolución son proporcionales a los cubos de los semiejes mayores a de la elipse.

3. ¿Sobre qué pidió ayuda Castelli a Galileo y cómo le ayudó?

Al dejar Galileo la universidad de Pisa, su puesto fue ocupado por su mejor alumno: Benedetto Castelli.

Poco tiempo después, a Galileo le llega una misiva de Castelli, quien le pedía ayuda para resolver una duda que le había planteado la duquesa Cristina de Lorena. La duda en cuestión era: que ella como mujer religiosa, había encontrado una oposición entre lo dicho en un pasaje de Josué y la teoría copernicana, ya que la Biblia nos dice que la tierra estaba quieta y Dios mandó detenerse al Sol, es decir, se pensaba que anteriormente el Sol estaba en movimiento (teoría geocéntrica); en cambio Copérnico afirmaba que la tierra se movia y el sol estaba quieto desde un principio (teoría heliocéntrica).

A pesar de los peligros que esto podía ocasionarle, decidió ayudar a Castelli mandándole una carta en la que exponia que, lo importante no son los ideales del momento, es decir, ya fuera la teoría heliocéntrica o la geocéntrica la que estuviera vigente, Dios los habría ayudado de la misma forma.